Bu dönem gördüğümüz Bilgisayar Mimarisi dersinde biraz Bilgisayar Aritmetiği’ne de değindik. Ders kapsamında birkaç çarpma ve bölme algoritmaları işledik. Bunlardan bir tanesi de Booth’s Multiplication Algorithm olarak geçen Booth’s çarpma algoritmasıydı.
Booth’s Algoritması genel olarak işaretli(signed) iki sayının ikiye tümleyen gösterimde çarpılmasını konu alıyor. Booth’s algoritmasının diğer çarpma algoritmalara göre avantajı ise daha az toplama ve çıkarma işleminin olmasıdır.
Burada, çarpan sayının bitleri çift olarak alınıyor, örneğin elimizde 1111 sayısı varsa 11 ve 11 birer çifttir. Birbirleriyle ardışık bit grupları (00,11) olduğu zaman, biz Booth’s algoritmasına göre avantajlı duruma geçiyoruz. Yani başka bir deyişle çarpan sayımızda birbirleriyle ardışık bit grupları yoksa (Örneğin: 010101) Booth’s algoritmasının diğer çarpma algoritmalarına göre avantajı olan daha az toplama ve çıkarma işleminden yararlanamıyoruz diyebiliriz.
Peki ne oluyorda birbiriyle ardışık bit grupları olduğu zaman avantaj elde ediyoruz ?
Öncelikle Booth’s algoritmasının işleyişini göstermek için bir tablodan yararlanabiliriz.
| xi | xi-1 | İşlem | yi |
|---|---|---|---|
| 0 | 0 | sadece kaydır | 0 |
| 1 | 1 | sadece kaydır | 0 |
| 1 | 0 | çıkar ve kaydır | 1’ |
| 0 | 1 | ekle ve kaydır | 1 |
Bu tabloda yi olarak gözüken değerler bizim recoded multiplier diyeceğimiz yeniden oluşturulmuş çarpan. Yani adından da anlaşılacağı üzere başlangıçtaki çarpma işlemimizdeki çarpanla bunu oluşturduktan sonra artık işimiz olmayacak diyebiliriz.
Bir örnekle recoded multiplier’ın nasıl üretildiğini gösterelim.
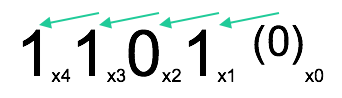
Örnek olarak bizim çarpan sayımız yukarıda görüldüğü gibi 1101 olsun. Burada dikkat edilmesi gereken, en anlamsız bitin (LSB) sağ tarafına hayali bir 0(x0) biti eklemek. Yani yeni çarpanımız 1101(0) sayısı. Şimdi yukarıdaki tabloya bakarak recoded multiplier’ımızı üretelim.
x1x0 sırasıyla 10 dolayısıyla y1=1’
x2x1=01 y2=1
x3x2=10 y3=1’
x4x3=11 y4=0
Yeni çarpan değerimiz böylelikle y4y3y2y1=0 1’ 1 1’ oldu.
Şimdi gelelim algoritmamıza. Örnek olarak elimizde A (çarpılan) -5 sayısı ve X (çarpan) -2 sayısı olsun. İşlemleri teker teker yukarıdaki tablomuzu göz önünde bulundurarak yapalım.

-5 ile -2’yi çarptığımızda toplamda 1 toplama ve 2 çıkartma işlemi yaparak sonucumuzu 10 olarak bulduk. Eğer Booth’s algoritmasını kullanmasaydık tahmin edeceğiniz üzere 4 toplama ve çıkartma işlemiyle sonucumuzu bulmuş olacaktık. Dolayısıyla Booth’s algoritması performans açısından daha iyi bir netice veriyor.
Umarım anlaşılır olmuştur, hoşça kalın..